Фильтрация - это очень просто

(аномальная фильтрация)

Вступление

        Данная работа явилась следствием длительных попыток автора снять сильную помеху, накладывающуюся на целевые времена - отражения от фундамента. Громадный объем безуспешных попыток заставил пересмотреть, казалось бы, очевидные вещи, сформулировать новые понятия и термины. По-видимому, именно с понятий и терминов следует начать разговор с читателем. Следует отметить, что все изложенное далее имеет смысл применять при обработке материалов МОГТ путем суммирования, что вовсе не обязательно, способ обойтись без суммирования, и, вместе с ним, и без каких-либо фильтраций, описан в работе Доминантная обработка.

        Прежде всего определим, с чем работает геофизик при обработке сейсмических данных. Он может иметь представление о строении разреза и составе основных волн, составляющих волновое поле. Но, для работы над материалом, он должен видеть эти волны невооруженным глазом. Если волна не видна, она для геофизика бесполезна, она для него просто не существует. Цель обработки - сделать нужные волны видимыми, а ненужные - невидимыми. Так что же такое видимая волна? Это не просто ось синфазности. Можно сгенерировать пару десятков трасс и заполнить их монохромными колебаниями. Осей синфазности можно провести столько, сколько фаз поместилось на трассе. Но, выделив ось синфазности и на мгновение отведя от нее взгляд, мы потеряем ее безвозвратно. Очевидно, для того, чтобы ось синфазности превратилась в волну, нужно что-то еще. Это "еще" - отличие ее от ближайшего окружения, "аномальность " ее в данном месте. Глаз видит сейсмограмму как набор аномалий, полезных и вредных, но именно аномалий, отличий от окружения. Существен только сам факт отличия, не количественные его характеристики. Малолетний хулиган с ножом в вагоне метро опасен для окружающих, капризный ребенок в супермаркете несколько раздражает остальных покупателей, но оба они - аномалии, хотя неприятности от них несоизмеримы. И неважно, что хулиган малолетний и любой взрослый превосходит его в физической силе. Важно, что в данный момент у него нож. Так и помеха. Она может быть энергетически слабой в общей энергии трассы, но, превышая ближайшее окружение, она делает невозможной работу с этим окружением.

        Итак, первое понятие - аномалия. Под этим термином в дальнейшем будем понимать любой объект на сейсмограмме, который глаз геофизика легко и уверенно выделяет на данном временном интервале. Аппарат, позволяющий менять свойства аномалии в ту или другую сторону будем называть аномальным фильтром, аппарат, позволяющий определять параметры аномального фильтра для решения конкретной задачи - аномальным спектром.

        Данную работу можно было бы назвать "Анти-Фурье". В дальнейшем на фактическом материале будут показаны особенности работы фильтров на основе Фурье-преобразований и аномальных фильтров. Здесь остановимся на главной характеристике Фурье (так для краткости будем называть использование преобразований Фурье для анализа и синтеза сейсмических материалов) - его безразличию к аномалиям, тяге к усредненным параметрам. Фурье подобен чиновнику-бюрократу. Сообщили ему частоту дискретизации материала - он определяет диапазон частот, от нуля до граничной. Сообщили длину интервала анализа - готов шаг спектра по частоте. Его не интересуют наши потребности, наши волны, задачи и прочая дребедень. Каждая точка спектра Фурье - усредненная амплитуда волны данной частоты по всему интервалу анализа, неважно, видим мы такую частоту на сейсмограмме, или нет, вообще, существует она физически, или это просто математический термин. Воздействие на любую точку спектра меняет каждую точку трассы, независимо от того, насколько она важна, дорога для нас. "Мавр сделал свое дело".

        Аномальный фильтр занимается только заданной ему задачей, своей аномалией. Он как пес-ищейка. Аномальный спектр как бы дает ему понюхать вещь, принадлежащую преступнику, затем команда "Фас" и он мчится вдоль трассы, пропуская без малейшего внимания интервалы, где заданной аномалии нет, и выгрызая найденную аномалию там, где она есть, без каких-либо дополнительных команд. Именно это свойство, индивидуальный подход к видимым объектам и делает работу с такими фильтрами надежной и комфортной. Однако следует ввести еще одно понятие, очень существенное для аномальных фильтров - "Доминанту", описанную в работе Доминантный анализ. Для эффективной работы аномальных фильтров недостаточно, чтобы аномалию видел глаз. Глаз - такая мощная вычислительная машина, с которой не может сравниться ни один созданный на настоящий момент алгоритм обработки. Для аномального фильтра необходимо, чтобы целевая аномалия доминировала над ближайшим окружением, т.е. чтобы определяющий ее характер был существенно сильнее, чем аналогичный параметр окружения. Другими словами, аномальные фильтры, так же, как и фильтры Фурье, бессильны перед зонами интерференции волн, близких по амплитуде и частоте, перед зонами, где нет доминирующего сигнала.

        Автор надеется, что ему удалось в достаточной степени для внимательного читателя раскрыть структуру аномальных приемов для практического использования. В противном случае автор готов разъяснять желающим любые аспекты аномального подхода к обработке. Для этого достаточно написать автору по адресу vbajbekov»собака»yandex.ru с темой "Фильтрация" или "Filtering" или на форуме http://www.maksim992.110mb.com/smf/index.php.

        Суть вопроса

        Наверное, фильтрация - одна из самых востребованных процедур при обработке сейсморазведочных материалов. И, наверное, одна из самых безуспешных. В общем случае процесс обработки начинается с выявления приповерхностных низкоскоростных и низкочастотных волн - помех. С этим, как правило, никаких проблем нет - они отчетливо видны невооруженным взглядом. Обычно они имеют вид регулярных волн, довольно локализованных, отличающихся от остальной записи частотой, амплитудой и/или направлением осей синфазности. Имеется большое количество средств, предназначенных для их подавления - одноканальные фильтры - низкочастотный, высокочастотный, полосовой, режекторный, многоканальные - двумерный или f-k фильтр. Наконец, мьютинг - грубое, с мясом,  уничтожение всей области существования помехи. Казалось бы, при таком обилии средств, главная трудность - выбрать одно средство из многих и расслабиться, пока средство работает. Ан нет! Каждый из этих способов, как солнце, имеет пятна.

Самый надежный - мьютинг - во-первых, меняет кратность при суммировании, во-вторых - область помехи может перемещаться при движении по профилю, что требует постоянного внимания оператора и достаточно частого изменения параметров мьютинга. Если пропустить момент выныривания помехи из области мьютинга, разрез моментально ухудшается.

С другими дела обстоят еще хуже. Чтобы фильтр сработал, ему нужно задать адекватные параметры, способные обеспечить его работоспособность. Поскольку все эти фильтры работают в частотной области, т.е. коррекция записи происходит путем изменения спектра Фурье, полученного по одной трассе или набору трасс, не так-то просто задать характеристику фильтра. Обычно действуют так:

1. Получают спектр той области записи, для которой предполагается конструкция фильтра.
2. Глядя на спектр и исходный материал, пытаются отождествить помеху с некоторой областью спектра.
3. Выделив область - кандидата, определяют параметры фильтра таким образом, чтобы область-кандидат после работы фильтра была существенно ослаблена. До сих пор все выглядело довольно просто, геофизик ощущал гордость от своего "всемогущества". Но затем наступает протрезвление:

·        Вопреки ожиданиям, помеха после фильтрации не исчезает. Можно добиться ее исчезновения, задав очень узкую полосу пропускания при полосовом фильтре, или широкие полосы вырезания при режекторном или односторонних фильтрах, но удовлетворения это не доставляет - области трассы, где никаких помех не наблюдалось, меняют свою форму, там появляются видимые колебания именно тех частот, которые мы стремились удалить. При двумерной фильтрации сейсмогрмма или разрез, в зависимости от того, что мы подвергли фильтрации, покрываются сеткой, также аналогичной по своим параметрам удаляемой нами помехе.

·        Мы начинаем метаться, меняем фильтры, разными способами ищем их параметры. Наиболее применяемые способы - получение спектра не по всей трассе или сейсмограмме, а по узкой полоске записи, содержащей практически одну помеху; определяем частоту помехи не по спектру, а по видимой частоте ее на трассе - все тщетно. Заканчивается этап фильтрации, в зависимости от опыта и темперамента оператора по-разному - он может ограничится одним из вариантов, когда помеха все-таки осталась, но, вроде бы, стала поменьше; он может отказаться от фильтрации вообще, ограничившись мьютингом; он может плюнуть на помеху, если она не ложится на времена целевого горизонта, смирившись с ее видимым присутствием на разрезе. Единственное, что объединяет любые решения оператора - помеха не удаляется с записи.

        Общее у всех вышеописанных вариантов - помеха осталась после фильтрации. Больше того, если остановились не на мьютинге, на всей трассе возникают искажения,большие или меньшие, в зависимости от жесткости примененного фильтра, но неизбежно . Никакие заклинания вроде применения "нуль-фазовых" фильтров ничего не меняют. "Нуль-фазовый" фильтр просто сохраняет первичный фазовый спектр. Меняется же форма колебаний, вплоть до количества фаз, когда говорить о смещении фаз просто бесполезно - неизвестно, с какой фазой нужно соизмерять это смещение.

        Ниже приведены результаты экспериментов с фильтрацией сильной волны-помехи, прямо накладывающейся на полезные отражения. Показаны три сейсмограммы, расположенные рядом вдоль профиля. Виден ярко выраженный цуг помех, начинающийся на времени около 2 сек и уходящий расширяющимся клином на большие времена. А целевое палеозойское отражение начинается в районе времени 2.9, где оно ныряет под помеху, но достаточно хорошо видно на удалениях, где цуг помехи исчерпан.

      Спектры Фурье тех же трех сейсмограмм. Мы видим, что нижняя граничная частота всех трех сейсмограмм находится около 10 гц.

         Ниже приведена одна трасса, на которой видна эта помеха на временах от 2.5 сек до конца трассы. Отчетливо видно, что частота ее существенно отличается от остальной записи, а амплитуда очень высока. Эта помеха делала невозможным получение разреза на целевых временах, как раз на том же интервале, что и помеха. В общей сумме она спокойно забивала сумму сигналов с трасс вне помехи.

        Попробуем применить к этой помехе фильтрацию в частотной области. Вся работа производилась в рамках системы СЦС-3, но это совершенно несущественно для предмета нашего разговора. В любой обрабатывающей системе результаты были бы теми же.

        Прямое измерение видимого периода помехи дает нам граничную частоту для фильтра - 12 герц ( не 10 герц, что примерно соответствует видимой частоте, а с некоторым запасом для реализации фильтра Фурье). Начинаем применять его.

        Те же три сейсмограммы, что и раньше, после фильтрации. Помеха просто не "чувствует" влияния фильтра.  В то же время на спектрах заданная частота уверенно вырезана, но это никак не проявилось на помехе.

        Посмотрим то же на отдельной трассе.

        Очевидно, кто-нибудь из читающих подумает, что я  просто дал слишком низкую граничную частоту для фильтра, нужно было дать ее с некоторым запасом. Я не настолько наивен, чтоы не знать этого, просто в моих архивах не нашлось таких иллюстраций. Я проводил эти эксперименты до частоты 18 герц, результат был тот же.

        Для понимания дальнейшего следут принять во внимание следующее: несмотря на большую амплитуду помехи, которую мы видим на рисунке, она вовсе не является чем-то чрезмерно сильным. Полоска между марками времени 2.0 и 2.5 показывает интервал нормировки. Общее усиление трассы   формируется таким образом, чтобы в пределах интервала нормировки амплитуды не имели перегрузки. Отчетливо видно, что амплитуды на временах меньших 2 сек обрезаны, т.е. существенно превышают амплитуду помехи, и это на интервале в несколько раз больше протяженности самой помехи. Т.о. энергетический вклад помехи в целую трассу невелик (помеха - аналог малолетнего хулигана с ножом). Она сильнее там, где находится, и только.

        Причина слабого эффекта от фильрации лежит в самой сущности преобразования Фурье и ему подобных преобразованиях. Спектр, конечно, связан с исходной трассой, но не аналогичен ему. Это в том смысле, что вмешательство в спектр может приводить к самым неожиданным последствиям. Когда мы вырезаем какую-то частоту или полосу частот в спектре, при обратном преобразовании из трассы вычитается гармонический сигнал заданной частоты и соответствующей параметрам фильтра амплитуды. Если мы задали режекторный фильтр с полным подавлением частоты f, значит, из всей трассы мы вычли синусоиду частоты f с амплитудой, вес которой в трассе соответствует значению этой частоты в общем спектре. Там, где помеха была, она немного ослабнет (немного, потому что самая сильная помеха в общей энергии трассы составляет небольшую часть из-за малого интервала ее действия, соответственно, в общем спектре ее амплитуда вовсе не соответствует амплитуде помехи в районе ее существования). На остальную же запись наложится синусоида частоты f со сдвигом на полпериода и ее влияние на запись будет поменьше на малых временах, где амплитуды трассы велики, и посильнее на временах больших, где амплитуды первичной записи падают вследствие геометрического расхождения волны.

    Вернемся к началу нашего этапа борьбы с сильной, отчетливо видимой помехой, попробуем подойти к ней по-другому. Попробуем сформулировать цели наших усилий.

1. Нужно выявить помеху. Если мы ее видим, следовательно, она при суммировании будет влиять на результат, естественно, ухудшая его. Трудно ожидать от помехи улучшения результата, тогда она называлась бы по-другому.
2. Нужно адекватно определить параметры помехи, чтобы применить их при настройке фильтра.
3. Нужно так преобразовать видимую запись, чтобы помеха на результат не влияла, или хотя бы влияла очень мало, и остальная запись в процессе уничтожения помехи совершенно не менялась бы. Когда, и если, нам понадобится менять запись в других интервалах, мы займемся этими интервалами отдельно, специально, независимо от работы с данной помехой. Будем держать котлеты отдельно от мух.

        Никаких трудностей на этом этапе не возникает.  Теперь самое время переходить в частотную область. Но зачем? Мы точно знаем, что хотим сделать, знаем, где это нужно сделать, а где ничего не трогать. Так какого рожна нам искать в частотной области, зачем нам преобразование Фурье?

        Любой программист средней руки за полчаса напишет программку, которая пройдется по трассе, определит видимые периоды, согласно заданным параметрам, и или пропустит их без изменения, или, в простейшем случае, обнулит. И все! Мы получаем автоматически настраиваемый мьютинг, работающий только там и тогда, когда натыкается на помеху (интервал записи, параметры которого соответствуют параметрам фильтра). Вся остальная запись остается абсолютно неприкосновенной. Ниже приведена работа подобного фильтра.

        Выраженный цуг помех практически исчез. На нижней (левой на рисунке) сейсмограмме можно различить годографы отраженных волн, пересекающих зону бывшей помехи. А что же произошло со спектрами? Ниже приводится сопоставление спектров Фурье до и после фильтрации.

Мы видим, что спектры практически не изменились, хотя изменения на сейсмограмме очевидны. Посмотрим, как работает фильтр на отдельной трассе.

Отчетливо видно ослабление помехи до полной неузнаваемости. Отличие формы остальной записи до и после фильтрации обусловлено разными вертикальным и горизонтальным масштабами рисунков до и после уничтожения помехи, что вызвано техническими причинами оцифровки рисунков. Фильтр абсолютно не трогает запись за пределами своей работы, это просто по определению.

        Рассмотрим полученный фильтр. Я задавал его параметры в количестве дискрет, помещающихся в полупериоде синусоиды. При подавлении низкочастотных волн он удаляет все полупериоды, в которые помещается хоть на одну дискрету больше, чем разрешено. При подавлении высокочастотных волн он удаляет все полупериоды, в которые помещается хоть на одну дискрету меньше, чем разрешено. При полосовой фильтрации он удаляет все полупериоды, в которые помещается хоть на одну дискрету меньше или больше, чем разрешено. За пределами этих запрещенных участков запись абсолютно неприкосновенна.  Можно задавать параметры фильтра не в дискретах, а прямо в частотах, программа сама пересчитывала эти частоты в дискреты. Разумеется, набор допустимых частот в задаваемых параметрах ограничен целым количеством дискрет, что программа обеспечивает автоматически, независимо от того, что думает об этом геофизик. Получился  фильтр с абсолютной крутизной характеристик, что совершенно немыслимо в спектральной области.

        Нужно отдавать себе отчет, что при обработке сейсмической трассы мы находимся вне физических полей, мы полностью в поле информационном. Здесь нет законов сохранения, нет инерции, массы и пр. Если в природе мы не можем остановить движение мгновенно (это потребовало бы бесконечной энергии), при обработке ничего не стоит оборвать запись, обнулить ее, скажем, при мьютинге. Поэтому заклинания о физической невозможности границ фильтра с абсолютной крутизной, применение при фильтрациях в частотной области разных антиалиасных приемов - это просто попытки справиться с недостатками преобразования Фурье, а не с физическими ограничениями.

        Данный подход одинаково эффективен для достижения любых целей улучшения записи. Можно сформировать фильтр, удаляющий высокие амплитуды, возникающие при воздействии внешних полей или неисправности питания. Если их не удалить, они порождают при суммировании гиперболические дуги на разрезе. Их вылавливают на трассах вручную и или отбраковывают такие трассы целиком, или обнуляют соответствующую часть записи данной трассы. Фильтр, настроенный на подавление амплитуд выше заданной, не пропустит ни одного всплеска, оставив неприкосновенной всю остальную запись.

        Вернемся еще раз к самому началу этапа фильтраций, к моменту выявления волны-помехи. На каком основании мы считаем ее помехой, где презумпция невиновности? Помехи могут быть разных типов, тем не менее мы уверенно и без колебаний идентифицируем их именно как помехи. Почему?

        Дело в том, что помеха и полезный сигнал выглядят по-разному. Именно выглядят, поэтому мы с первого взгляда опознаем их. Они - аномалия на регулярном поле. По этому признаку я и назвал свои фильтры аномальными. Какой бы природы ни была аномалия - по частоте, амплитуде или направлению осей синфазности, именно отличие этих признаков от окружающей области и делает ее помехой.

        Разобравшись с процессом выявления помех и получив средство эффективного их подавления, попробуем облегчить себе жизнь, создать условия покомфортнее в момент определения параметров фильтра. В этом отношении спектр Фурье очень удобен. Скажем, если профиль проходит под высоковольтной линией, на спектре мы отчетливо видим преобладающую частоту. Нет никаких проблем, чтобы задать параметры фильтра и подавить помеху. В этом случае, в отличие от описанных ранее, фильтрация в частотной области очень удобна и эффективна. Дело в том, что промышленная помеха, в отличие от сейсмической, присутствует на всем интервале трассы, да еще и существенно превосходит остальную запись по амплитуде. Сейсмическая же помеха, да и любая сейсмическая волна, существует только в ограниченном интервале времени и вклад ее в общую энергию трассы очень невелик. С такими волнами преобразование Фурье работать просто не может. Каждая точка спектра Фурье относится ко всем без исключения точкам трассы во временной области, а каждая точка трассы - ко всем без исключения точкам спектра. Невозможно через спектр преобразовать только часть трассы, как и через запись на трассе преобразовать только определенную часть спектра. Однако хотелось бы получить инструмент, делающий определение свойств отдельных волн таким же простым и удобным, как и спектр Фурье, только без его недостатков.

        Попробуем получить гистограмму видимых периодов на всем интервале трассы. Здесь мы, наверное, увидим, во-первых, граничные значения, т.е. наименьший и наибольший периоды, что соответствует наибольшей и наименьшей видимым частотам. Наверное, выделится и основная частота полезной записи, регулярных волн. Частота помехи вряд ли будет ярко выражена на гистограмме по той же причине, что и в спектре Фурье - ее область существования невелика и намного меньше, чем интервал трассы. Единственное, что покажет нам достаточно уверенно некоторый параметр помехи - низшая граничная частота на гистограмме. Она, скорее всего, принадлежит помехе, но для фильтрации этой информации маловато, нужна граница между помехой и полезными волнами а ее мы пока получить не можем.

    Порассуждаем дальше, попробуем недостаток волн-помех - ограниченный интервал их существования, превратить в свойство полезное. В пределах всей трассы энергия волн существенно меняется, а частота составляет две основных совокупности - низкочастотные волны (помехи) и остальная запись - полезные волны, микросейсмы и прочий фон. Если мы построим не просто гистограмму, где выражается количество периодов разных длительностей, а гистограмму, где суммируются амплитуды этих периодов, она понесет информации несколько больше, чем в первом случае, но все еще недостаточно для определения параметров фильтра. А вот если мы эту гистограмму разделим на дисперсию амплитуд для каждого видимого периода, картина в корне меняется. Именно то, что помеха ограничена во времени существования, делает дисперсию ее амплитуд малой, в отличе от остальной записи, где амплитуды меняются не на один порядок. Такая гистограмма уверенно выделит большим максимумом частоту регулярной низкоскоростной помехи. Второй максимум  амплитуды даст основная частота регулярного сейсмического фона. По аналогии с названием спектра Фурье я назвал такие гистограммы аномальными спектрами. Они очень легко и несравненно быстрее, чем спектры Фурье, получаются, и информация, полученная от них, безусловно определяет точную и эффективную работу аномальных фильтров. Ниже показан пример применения подобного спектра.

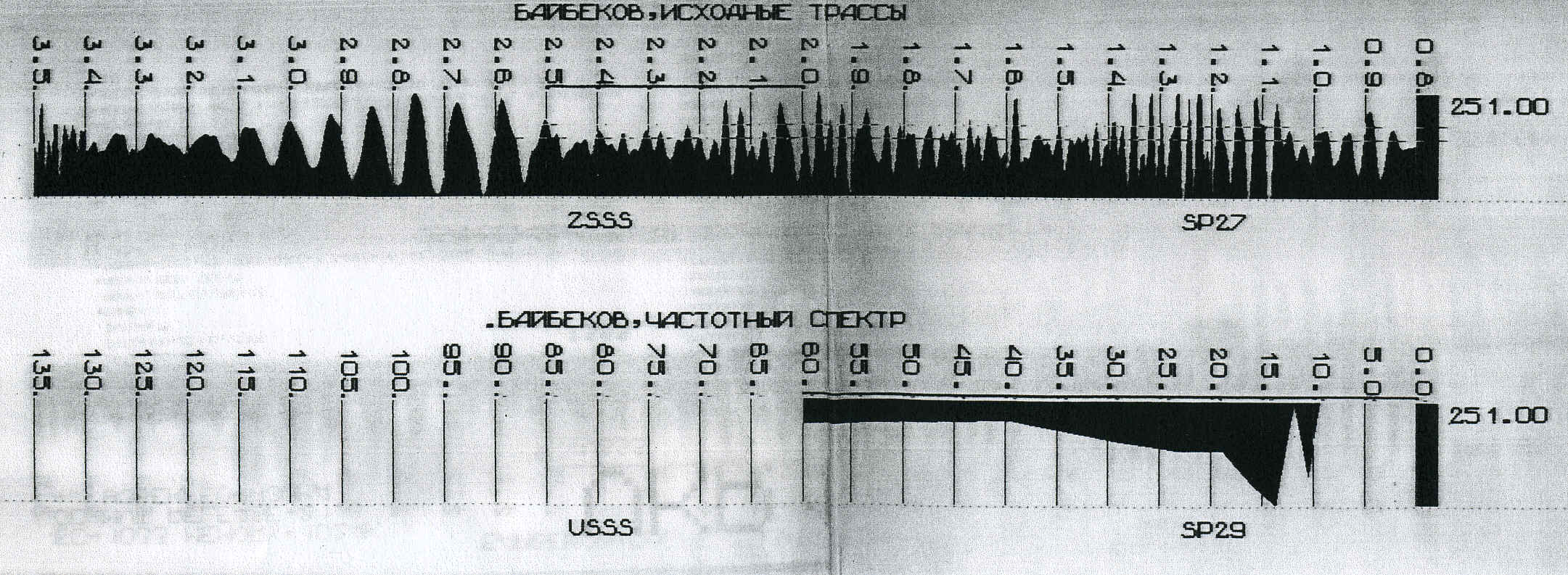
        Пик на спектре в районе 10-12 герц как раз и характеризует волну помеху. Он прекрасно выражен, как и было описано выше, и вполне четко определяет параметры фильтра. Далее смотрим, что происходит с трассой и спектром после фильтрации фильтром Фурье и аномальным фильтром.

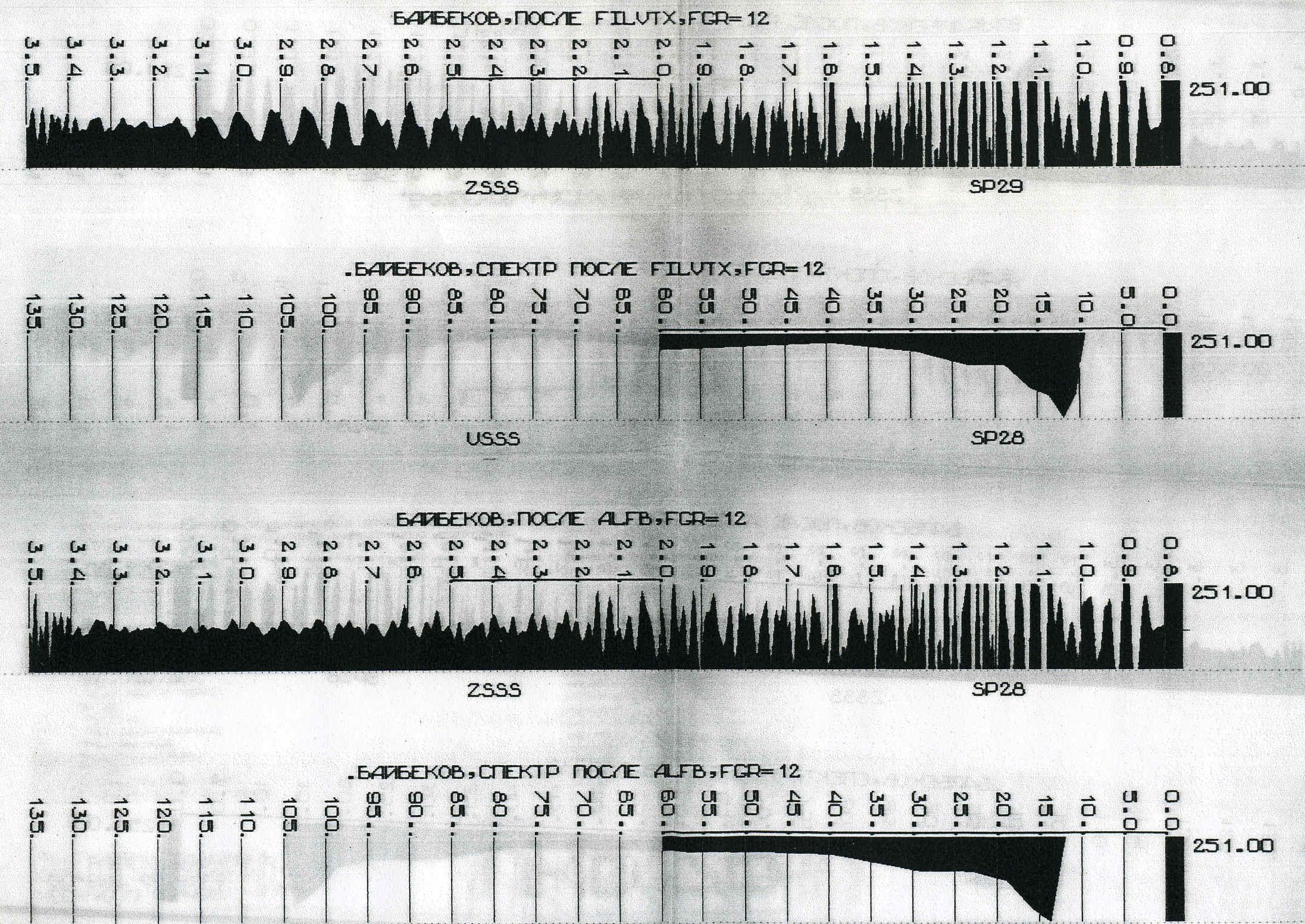
        После фильтрации в частотной области помеха на исчезла, хотя в спектре Фурье, как мы помним, полный ажур, спектр изменился в нужную сторону. Аномальный же спектр показывает слияние частот полезного сигнала и помехи, нижняя граница стала даже ниже, чем на исходном материале. Неверная работа фильтра, также, как и неоптимальное суммирование ОГТ всегда приводит к понижению нижней граничной частоты.

    После аномального фильтра мы видим полное сопадение картин во временной и спектральной областях. Спектральной я в данном случае называю не пространство Фурье, а пространство аномального фильтра. Мы видим, как исчезла помеха и совершенно чисто исчезло ее проявление на спектре. Остальная часть спектра, так же, как и нефильтруемая часть трассы, остались без каких-либо изменений.

        Процедура получения аномального спектра и запуск аномального фильтра с полученными из спектра параметрами могут быть легко объединены в единой программе. Больше того, они дают прямое указание, даст ли фильтрация эффект. Если на записи нет помехи, четко выраженной по частоте и локализованной по времени, спектр не даст четко выраженного максимума в низкочастотной области спектра, применение фильтра в этом случае бессмысленно, хотя даже в этом случае аномальный фильтр не навредит, не вмешается в полезную запись.

        В заключение автор приносит извинения за низкое качество иллюстративных материалов. Других нет по техническим причинам. Но любой заинтересованный читатель легко воспроизведет описанные эксперименты с фильтрацией "по Фурье" на своем материале. Повторяю основные моменты экспериментов:

1. Выбирается сейсмограмма(ы) с ярко выраженными цугами помех.
2. Считаются и визуализируются спектры, полученные по этим сейсмограммам до фильтрации.
3. Любым, самым любимым методом определяются параметры фильтра.
4. Любым, самым любимым фильтром производится фильтрация.
5. Визуализируются отфильтрованные сейсмограммы.
6. Считаются и визуализируются спектры Фурье после фильтрации.

    Далее - перечитывание и осмысление вышеизложенного заново, с учетом полученных своими руками результатов.

    Мнения и предложения по конструированию аномальных фильтров будут с благодарностью приняты автором. Возникшие при чтении или попытке реализовать изложенные здесь идеи вопросы и сложности вполне обсуждаемы, и, надеюсь, решаемы. Для этого достаточно написать автору по адресу vbajbekov»собака»yandex.ru с темой "Фильтрация" или "Filtering" или на форуме http://www.maksim992.110mb.com/smf/index.php.