К вопросу о природе отраженных сейсмических волн

Прежде, чем приступить к работе, рассмотрим жизнь посланного в среду акустического сигнала и события, его при этом сопровождающие. Если среда полностью однородная, дело выглядит так: по мере продвижения упругих возмущений среды внутрь ее мы можем увидеть следующее – перед возмущением среда спокойна просто потому, что сигнал туда еще не дошел, за прошедшим возмущением среда также спокойна. Это описать сложнее. Согласно принципу Гюйгенса каждая точка среды является равноправным самостоятельным источником возмущений, порождающим в однородной среде сферическую волну. Так вот множество точек, порождая множество таких элементарных волн создают интерференционную картину, где, вследствие фазовых сдвигов между собой, колебания от разных точек полностью друг друга подавляют. И только в области активных фаз сигнала в среде идет сферическая зона возмущений, которую мы можем регистрировать нашей аппаратурой.

Однако, жизнь сложна, и реально однородных сред не существует. Рассмотрим, для начала, двуслойную среду, где каждый слой однороден, но друг от друга они отличаются акустической жесткостью. Внутри каждого слоя картина полностью соответствует описанной выше, а вот в области границы возникает новый эффект. За фронтом волны, сзади, исчезает полное взаимное подавление, т.к. частицы разных слоев реагируют на сигнал по-разному. В результате в обратную сторону, назад, начнет распространяться возмущение, амплитуда которого зависит от соотношения акустических жесткостей слоев. Если граница большая и плоская, мы получаем отраженную волну, если неоднородность акустической жесткости локальная, получаем волну  дифрагированную.

По первоначальному направлению движения сигнала идет прямая волна, назад – отраженная или дифрагированная. Усложняя модель, наращивая количество границ или слоев, варьируя величинами акустических жесткостей, мы получим сложную, но очень похожую на реальные сейсмограммы, волновую картину. Можно ли с ней работать? Что мы хотим из нее получить? Работать можно, получить хотим положение и, желательно, параметры границ акустической жесткости. Рассмотренный процесс математически описывается процедурой свертки сигнала с импульсной сейсмограммой – математическим представлением набора границ (неоднородностей) в среде. Заметим, что результат свертки соответствует именно волнам, идущим назад, волна, идущая вперед, просто постепенно теряет энергию как за счет расширения сферического фронта, так и за счет энергии отраженных сигналов – границы через себя пропускают только часть подходящей к ним энергии, остальная возвращается назад. Следует особо отметить – указанный процесс действует повсеместно, независимо от того, занимаемся мы первичным сигналом или его порождениями, идет ли волна внутрь среды или возвращается к источнику возбуждения. Отраженная волна после своего возникновения ведет себя точно так же, как первичная и на однородностях и границах, в свою очередь, порождает вторично отраженные или дифрагированные волны.

Процедура, обратная свертке – корреляция должна дать нам возможность получить из записи полученных колебаний импульсную сейсмограмму – цель сейсморазведочных работ, но для этого небходимо знать сигнал, с которым сворачивалась импульсная сейсмограмма.

Подведем итоги:

1. Существует некая импульсная сейсмограмма, отражающая распределение акустических жесткостей в земной коре в районе исследований. Она однозначно связана со средой.
2. Мы посылаем некий сигнал, который сворачивается с этой импульсной сейсмограммой, порождая поле отраженных волн. Оба первых пункта, разумеется, не среда с колебаниями, но достаточно близкая к ней математическая модель. Но:
3. В природе при прохождении прямой волны возникает некая пакость в виде приповерхностных помех, накладывающихся на поле отраженных волн и искажающая их. Эти помехи моделью не учитываются. Естественно, волны, которые не побывали в глубине, не могут дать нам информацию о нижних этажах разреза. С этой пакостью мы должны бороться специальными методами – фильтрациями, мьютингом, выбором оптимальных систем наблюдений, чтобы очистить запись, приблизить ее к модели.
4. Постоянно существуют еще и микросейсмы – пакость поменьше, которая также накладывается на поле отраженных волн и искажает его. С ней мы должны боремся статистическим накоплением сигналов и увеличением энергии посылаемого в землю сигнала с той же целью.
5. Если нам удастся победить помехи и узнать истинную форму посылаемого импульса, мы сможем прокоррелировать очищенное волновое поле с сигналом и получить на выходе импульсную сейсмограмму, после чего с чистой совестью пересчитывать честно заработанные деньги. Если нет – совесть наша будет нечиста.

  Существуют методы узнать сигнал, с которым сворачивалась импульсная сейсмограмма и прокоррелировать сейсмограмму с ним – в частности, обратная фильтрация. Может быть, она и работала бы неплохо, если бы мы могли эффективно справляться с помехами, и, главное, если бы сигнал не менялся на своем пути в среду. Однако общепризнано и легко увидеть это на материалах ВСП, что сигнал меняется, в частности, понижается его эффективная частота «за счет более сильного поглощения высокочастотной составляющей». Но переменный сигнал – смерть деконволюции и модели отраженных волн как результата свертки.

  Я не буду здесь касаться причин, почему результаты сейсморазведочных работ недостаточно хорошо в ряде случаев совпадают с реальным строением геологического разреза. Причин этих масса, и удивительно, как вообще удается методу ОГТ получать удовлетворительные результаты при столь наглом попрании своих собственных теоретических основ. Я рассматривал это попрание в работе Доминантная обработка.

    В данном опусе я коснусь только некоторых фактов, не укладывающихся в вышеприведенные 5 пунктов. Пока что добавлю к ним еще общепризнанные, казалось бы, не требующие доказательств или проверок утверждения:

1. По мере прохождения сквозь земную толщу возбуждающий импульс вследствие неодинакового поглощения  на разных частотах теряет свою высокочастотную составляющую, что приводит и  к снижению видимой частоты глубоких отражений,
2. Волновое поле в значительной своей части представлено кратными волнами, как простыми, так и частично-кратными, образованными как дневной поверхностью, так и границами внутри среды.
3. Кроме естественного ослабления энергии первичного импульса вследствие геометрического расхождения, он теряет энергию при каждом акте прохождения сквозь акустическую границу, частично отдавая ее в качестве отраженной волны. Остаток проходит сквозь границу, естественно, ослабленный, ведь не может остаток равняться целому.

        Ниже я опишу одну лишь скважину с ВСП и то, что я с ней проделывал. Естественно, одна скважина не является представительным материалом, но уважающая себя теория должна обязательно удовлетворять всем имеющимся наблюдениям, да еще и предсказывать некоторые вещи, покуда не наблюденные. Если вдруг объяснить изложенные ниже эффекты традиционными методами нельзя, что-то с теорией не в порядке.

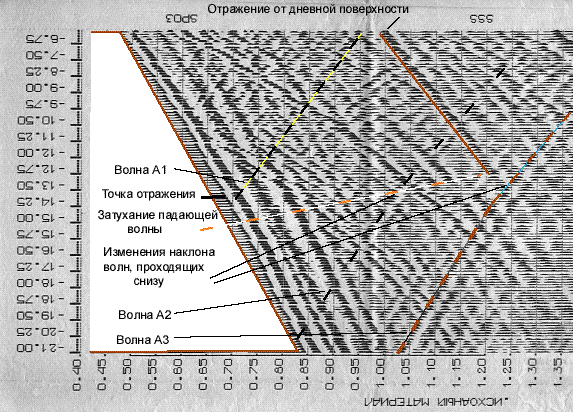
Рассмотрим данный рисунок. В точке отражения порождается волна А1, которая, отражаясь от дневной поверхности, создает вторичную падающую волну, названную на нижеследующих рисунках Апад. Ниже первой точки отражения существуют еще границы, от которых исходят волны А2 и А3. Обычная, тривиальная картина. Однако, рассмотрим ее повнимательнее. На уровне 1300 - 1400 м от поверхности мы видим обычные события - отрыв от цуга падающей волны первого отражения А1 и на той же глубине изменение наклона отражений А2 и А3. Однако, вопреки теории отраженных волн, ни волна А2, ни волна А3 не дают отражений от границы вниз. С одной стороны на них видно влияние границы - изменение наклона годографа прямо указывает на изменение скорости в среде, с другой стороны, изменение скорости должно породить значимый коэффициент отражения, а этого нет. В то же время на той же глубине отчетливо затухает падающая вниз волна Апад, которая по теории должна и отразиться вверх, рождая кратную волну, и пройти вниз, изменив наклон соответственно закону преломления. Получается, что граница - родитель волны А1 действует на приходящие к ней волны избирательно - сначала для падающей волны возбуждающего импульса совершенно естественно, в соответствии с общепринятыми взглядами, создав отражение, а затем начинает капризничать - пропуская сквозь себя волны снизу как преломленные, но не отражая их вниз. А уж с падающей кратнообразующей волной Апад поступает совершенно подло - вообще не пропускает  вниз и не отражает вверх, т.е поглощает. Интересно еще и то, что прошедшие через границу волны А2 и А3 имеют параллельные между собой  годографы, но эти годографы не параллельны волне А1, первичной отраженной волне.

        Ну, последнее с некоторой натяжкой объяснить несложно, можно предположить, что граница А1 не параллельна остальным границам, которые между собой близки к параллельным. Подойдя снизу к границе параллельно между собой, они и дальше остаются параллельными. Однако остальные факты требуют объяснения более серьезного, т.к. они прямо противоречат общей теории отраженных волн. Вспомним главное ее положение - скачок акустической жесткости вызывает явление отражения. Здесь нет никаких зависимостей от свойств сигнала, направления подхода  или чего-либо еще. Тот же скачок акустической жесткости определяет и преломление - изменение кажущейся скорости годографа волны. Так вот на пути снизу вверх  преломление происходит, т.е. наличие скачка жесткости сомнений не вызывает, а отражений вниз нет. Как же быть со сверткой сигнала с импульсной сейсмограммой? Как быть со спектральным анализом волнового поля, с деконволюцией, полностью базирующимся на модели свертки? А поглощение падающей волны Апад своим родным контактом, именно тем, на котором родилась отраженная А1 волна-родитель падающей, потенциально кратно-образующей? Если это так, то откуда возьмутся кратные волны? А ведь борьба с кратными волнами - это базис всего метода общей глубинной точки - основного метода сейсморазведки в настоящее время. Интересно, что поглощение (подавление) может объясняться эффектом акустического резонансного поглощения (АРП), описанного Г.А. Гликманом в работе «спектральная сейсморазведка - истоки и следствия » в главе 3.

        Ниже показан анализ волнового поля, проделанный с применением аномальных фильтров (Аномальная фильтрация). Здесь скажу только, что аномальные фильтры – это фильтры с бесконечной крутизной, не использующие преобразования Фурье, хотя точность выставления в них границ фильтрации аналогично фильтрам Фурье зависит от дискретности представления сигнала. С помощью таких фильтров возможно последовательно, слой за слоем вырезать некоторые области частот, низких, высоких, просто частотный полос для анализа интересующих нас волн. В данном случае я вырезал низкие частоты до тех пор, пока не пропадала Апад - падающая кратнообразующая волна, а восходящие волны остались. Частота кодирования исходного материала - 250 гц. Параметр фильтра в дискретах указывается слева на поле рисунка. Обработка здесь и в других местах велась в системе СЦС3. Параметр фильтра расшифровывается  так : ALFB означает "аномальный низкочастотный фильтр Байбекова", "D" - означает, что параметр задан в дискретах, 20 - граничное количество дискрет в полупериоде. Формула для пересчета параметра в граничную частоту - Fгр=1000/(D*4). На представленных ниже рисунках следует следить за поведением волны Апад.

Пропущены частоты выше ~12.5 герц, остальные подавлены

 

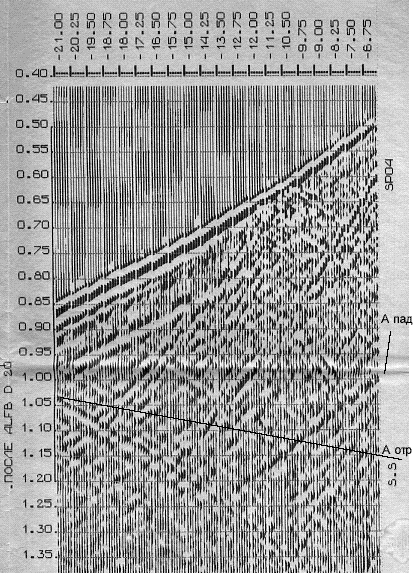
   Рисунок соответствует фильтру с граничной величиной видимого периода 20 дискрет. Картина полностью соответствует исходному материалу, т.е. в волновом поле частоты ниже 12.5 герц отсутствуют.

Частоты выше ~14 герц

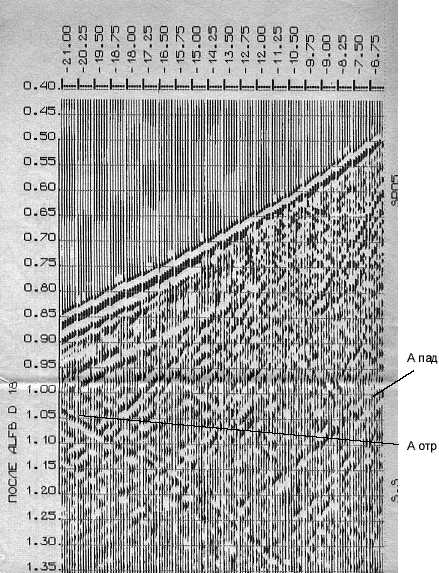
Происходит частичное ослабление падающей волны. Отраженная остается без изменений.

Частоты выше ~15,6 герц

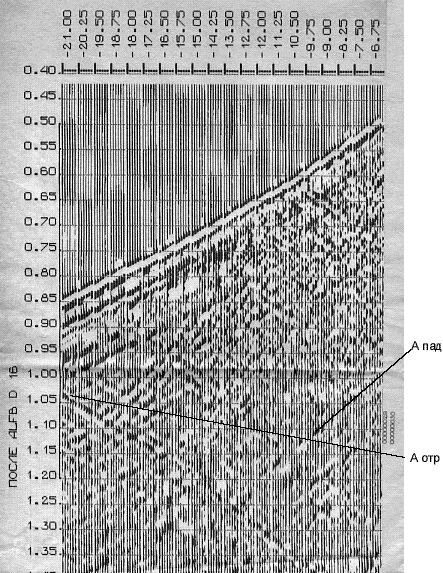
Происходит существенное ослабление падающей волны. Отраженная остается без изменений.

Частоты выше ~16,7 герц

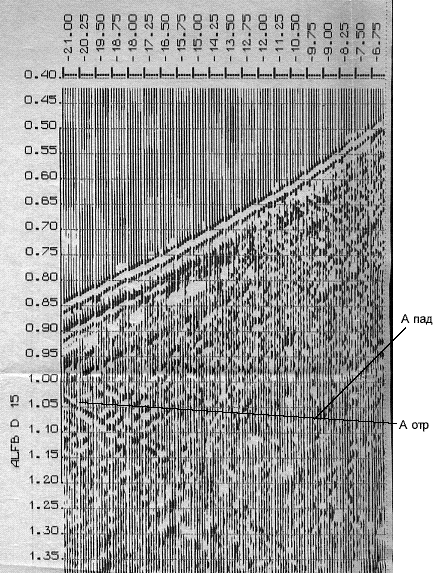
        Происходит полное ослабление падающей волны. Отраженная ослабляется выше границы и не меняется ниже.

        Такая избирательность совершенно не предусмотрена теорией отражений. Попробуем сделать некоторые предположения, которые укладывались  бы в наблюдаемую картину.

Несколько слов о физических свойствах отражающих границ - граница А1 является мощным слоем туронских глин, очень тонкодисперсных, пластичных и однородных. Граница А2 - очень плотные  сенонские аргиллиты, граница А3 - бухарские известняки. Обе нижние границы - жесткие, твердые, не пластичные. Далее мы попробуем связать эти свойства с параметрами отражений (восходящих волн).

        Рассмотрим строение волн, наблюдаемых нами на разрезе ВСП (впрочем, это применимо и к любой сейсмограмме, полученной импульсным источником). Каждый волновой пакет характеризуется только "несущей" частотой, амплитудой первой фазы и декрементом затухания. Слово "несущей" взято в кавычки, чтобы подчеркнуть, что это слово имеет не тот смысл, что несущая частота в радиотехнике, где она каким-то образом   модулируется. Сейсмические волны могут интерферировать с другими волнами и затухать, но не модулироваться.

        На каждой трассе информативная запись начинается с импульса падающей (прямой) волны, испускаемой источником. Естественно, свойства этого импульса определены условиями, которые создает зона непосредственного возбуждения. Каждая зона возбуждения состоит из более или менее обширной зоны пластической деформации (зоны, где среда разрушается, сминается, короче, деформируется) и, вне ее, зоны упругой деформации, где разрушения скелета породы не происходит, а только частицы смещаются из состояния равновесия с последующим возвращением назад. Если воздействие на среду превосходит предел ее прочности, энергия уходит на деформацию. Только после падения напряженности сейсмического поля ниже предела прочности породы возникают и распространяются в среду упругие колебания. Среда не может передавать колебания, мощность которых превосходит предел ее прочности. Значит ли это, что энергия звуковых волн в среде не зависит от мощности источника? И да, и нет. Напряженность поля действительно, зависит только от свойств среды (разумеется, если, все-таки мощность источника создает напряженность, превосходящую предел прочности породы), а не от мощности источника. А вот форма передового импульса от мощности источника все-таки зависит, т.к. излучающим объектом при импульсном воздействии является псевдосфера, ограничивающая зону пластической деформации, а объем ее зависит от мощности заряда. Каждая точка этой псевдосферы, по принципу Гюйгенса, излучает колебания во все стороны и наблюдаемая нами картина - интегральная сумма излучений всех точек псевдосферы. Чем больше мощность заряда, тем больше объем зоны пластической деформации и тем ниже несущая частота прямой волны. Итак, самый первый полупериод прямой волны определен условиями зоны возбуждения, и только ими. Разумеется, на форму флияют характеристики сейсмоприемников, но этого аспекта мы здесь касаться не будем.

        Представим себе процесс прохождения звуковой волны через слоистую среду. Падающий на границу импульс воздействует на нее и она начинает колебаться в вынужденном режиме до тех пор, пока не пройдет передовая фаза сжатия возбуждающего импульса. Граница напрягается, ее скелет выходит из состояния равновесия. С исчезновением вынуждающего давления граница в режиме свободных колебаний возвращается в исходное состояние, естественно, также в колебательном затухающем режиме. При этом процесс успокоения уже не зависит от свойств возбудившего границу импульса, в особенности от его "несущей" частоты, а только от степени отклонения границы от состояния равновесия и ее собственного декремента затухания. Аналогом этого явления может служить раскачивание качелей – амплитуда зависит от толчка, а частота раскачиваний – только от длины веревки, на которой качели повешены. И вот главное, чему и посвящена данная работа. Представляется, что каждая граница имеет свою индивидуальную "несущую" частоту. Колебания успокаивающейся среды распространяются, опять же по принципу Гюйгенса, во все стороны. Нас, главным образом, интересуют два направления - вниз и вверх. Вверх идет то, что мы называем отраженными волнами, а вниз, вслед возбуждающему импульсу, идут такие же колебания, как и вверх, создавая, подобно кометному хвосту, следующее за ним обрамление. Общепризнанное понижение частоты с глубиной, по моему мнению, объясняется не избирательным поглощением энергии на высоких частотах, а наличием этого, все более обогащающегося хвоста, накапливающего свободные колебания всех пройденных границ акустической жесткости со случайными амплитудами и сдвигом фаз. Любое несинфазное суммирование колебаний, не совпадающих по частоте между собой, вызывает понижение видимой частоты суммы.

         Теперь оставим в покое колебания, идущие вниз, в среду, и займемся возвращающимися к дневной поверхности колебаниями. В описываемом процессе нет отражения, только собственные колебания успокаивающейся границы.   Поэтому нет и влияния на форму восходящих колебаний формы падающего импульса. Он необратимо ушел в землю, сделав свое дело, и о нем можно забыть. Волны, идущие  вверх, зависят только от свойств границы, их породившей.  Естественно ожидать от пластичных пород частот ниже, чем от жестких, твердых. Если это так, мы должны зафиксировать различия частотных свойств различных восходящих волн. Но ведь именно это мы только что и наблюдали! Ограничивая прохождение через фильтр определенных частот, мы видим как одни волны меняют свои свойства, другие - нет. По устоявшейся теории могло бы быть только уменьшение частоты с увеличением глубины отражающей волны, связанное с понижением частоты прямой волны, а мы видим картину обратную. Ослаблены, т.е. обладающие более низкой частотой,  именно волны верхнего этажа, волны нижнего спокойно проходят через фильтр, следовательно, их несущая частота выше, чем у верхних.

        Таким образом, в рамках рассматриваемой гипотезы, границы раздела акустических свойств выступают в роли не отражателей, как обычно считается, а в качестве резонаторов, возбуждаемых прямой волной. А свойства отражателя и резонатора отличаются очень существенно.

        Прежде всего, для резонаторов совершенно неприменим математический аппарат свертки. Из пары - сигнал-импульсная сейсмограмма - выпадает сигнал. Цель сейсморазведки остается прежней - получение импульсной сейсмограммы, а весь традиционный аппарат обработки, построенный на стабильности сигнала, оказывается несостоятельным. Отсутствие свертки делает бессмысленной работу в частотной области, любые виды конволюций и деконволюций. Появляются принципиально новые эффекты. Мы убедились на приведенных рисунках, что восходящие волны отличаются частотными свойствами. Грубо говоря, это аналогично окрашиванию белого света при прохождении через цветные фильтры. Но, в этом случае имеется еще одна особенность - цветной фильтр по-разному пропускает белый свет и цветной. Из белого цвета цветной фильтр пропускает тот цвет, на который он настроен, а вот пропускание цветного цвета, не совпадающего с цветом фильтра, не так четко определено. Цветной фильтр может вообще не пропускать свет другого цвета, может пропускать частично, с изменением цветовых характеристик выхода. Наконец, раз мы имеем дело с колебательными процессами, можно воспользоваться аналогией с электрическим колебательным контуром. Его активное сопротивление является аналогом поглощения сейсмических волн в среде, а вот реактивное, как известно, максимальное на резонансной частоте колебателного контура, определяет реакцию пласта на подход волны с частотой резонанса. Это мы и наблюдаем при затухании падающей волны Апад на самом первом рисунке, не подверженном никаким фильтрующим воздействиям. Эта волна порождена дневной поверхностью, границей со столь высоким коэффициентом отражения, что она практически на меняет подходящий сигнал за исключением направления его движения. Характеристики волны А1 формируются только резонансными свойствами отражающей границы, границы, породившей волну-родителя этой падающей волны. Если падающий импульс мы можем считать аналогом белого цвета, отраженная волна – окрашена в цвет, соответсвующий «собственной частоте» границы. Из этих рассуждений и приведенной картинки может следовать еще один очень существенный вывод, режущий ухо  - отсутствие в принципе кратных волн. Мы видим невооруженным глазом, как волна, вернувшаяся к границе-родителю, волна сильная, исчезает полностью. Если эффект, наблюдаемый нами на приведенном монтаже ВСП существует повсеместно, кратная волна поглощается самой кратнообразующей границей и на поверхность вообще не выходит. Этот вопрос может быть решен только изучением множества скважин, возможностью чего я не обладаю. Поэтому утверждение о полном отсутствии кратных волн остается гипотетическим, что не касается остальных фактов и выводов, описанных выше. Однако еще в семидесятые годы Т.М. Епинатьева, человек, достаточно разбираюшийся в сейсморазведке, на своих семинарах прямо утверждала, что кратные волны – миф. Не нужно забывать также, что коэфициенты отражения в реальных средах достаточно малы, чтобы для кратных волн, когда суммарный коэфициент равен произведению коэфициентов границ, пройденных волной, чего вполне лостаточно, чтобы перевести уровень кратных волн в соизмеримый с микросейсмами.

        Отдельным, очень интересным, вопросом является применение вибросейсмических источников. Если для импульсных источников, как было показано выше, структура падающей волны практически неуправляема, цвет импульса-посылки всегда белый, для вибросейса это утверждение неприменимо. Появляется принципиальная возможность управлением, настройкой источника на решение конкретной геологической задачи, на конкретный глубинный объект.

Резюме

           

        Приведенные материалы позволяют утверждать, что частотные свойства сейсмических волн прямо отражают свойства акустической границы, и слабо связаны со свойствами источника возбуждения. Эти свойства могут быть использованы для избирательной обработки каждой акустической границы индивидуально. Показаны причины низкой эффективности методов обработки, использующих спектральные преобразования, их необоснованность в связи с необоснованностью модели свертки постоянного сигнала с импульсной сейсмограммой.

        Высказано предположение о принципиальном отсутствии кратных волн, модель которых полностью стоит на аппарате отражения, аппарате свертки. Дальнейшие исследования могут решить судьбу этого предположения.

        Предполагается резкое расширение возможностей методических приемов, связанных с вибросейсмическим возбуждением колебаний. Здесь также требуются дальнейшие нетривиальные исследования, пересмотр подходов к количеству и качеству энергии, посылаемой источником в среду.

            Обсуждая резонансные явления, было бы неправильно не упомянуть работы А.Г. Гликмана http://www.newgeophys.spb.ru/. Им поставлены очень интересные эксперименты по выявлению собственных частот отражающих объектов. Отдавая должное остроумие опытов, автор категорически не согласен с основными выводами г. Гликмана, а именно:

1.      Что акустический сигнал не распространяется в среду, а идет только вдоль поверхности.

2.      Что резонаторами являются только элементы геологического разреза, одна граница которых совпадает с дневной поверхностью, т.е. исключаются слои, на поверхность не выходящие.

3.      Что ортогональная составляющая волнового поля, зафиксированная г. Гликманом и поперечные волны – одно и то же.

4.      Что скорости продольной и поперечной волн равны между собой.

5.      Что вообще скорость акустических волн постоянна и равна 2500 м/сек

Более детально эти расхождения автор рассмотрит в отдельной статье.

Автор с благодарностью примет любые замечания и возражения непосредственно по электронной почте по адресу vbajbekov»собака»yandex.ru  с темой «Резонаторы» или на форуме http://www.maksim992.110mb.com/smf/index.php.